Chapter 1: Understanding E=mc²

E=mc² stands as one of the most recognized equations in the realm of physics, familiar to nearly anyone who has encountered the subject. But what does this equation truly signify, and what is its importance? Let's dive into this topic.

To aid our exploration, we turn to Albert Einstein, whose pivotal 1905 paper titled "Does the Inertia of a Body Depend Upon Its Energy Content?" introduced this iconic formula.

Inertia refers to the property of objects to maintain their velocity in the absence of external forces, resisting any change in motion when a force is applied. Greater mass results in increased inertia, necessitating more force for acceleration. Thus, the inertia of an object is directly linked to its inertial mass.

Another essential concept is momentum, defined as the "quantity of motion." Momentum is influenced by velocity, and for massive objects, it is also related to the object's inertial mass. Notably, momentum is relative; its value varies depending on the observer's frame of reference. For an observer moving with the object, the object appears stationary, resulting in zero momentum.

Now, consider a spacecraft that emits two strong beams of photons in opposite directions. Photons, being massless particles of light, still possess momentum.

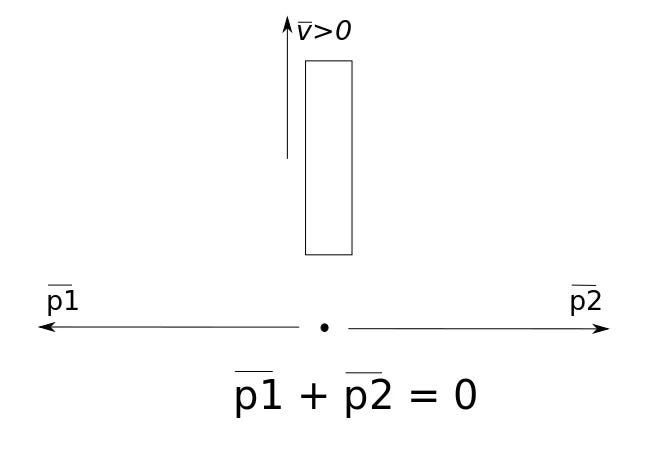
From the perspective of the spacecraft at the moment it emits the light beams, its momentum remains unchanged. This is because the momentums of the two photons, moving in opposite directions, effectively cancel each other out.

However, if we view this scenario from the spacecraft's frame of reference, we observe that the photons are traveling apart from each other.

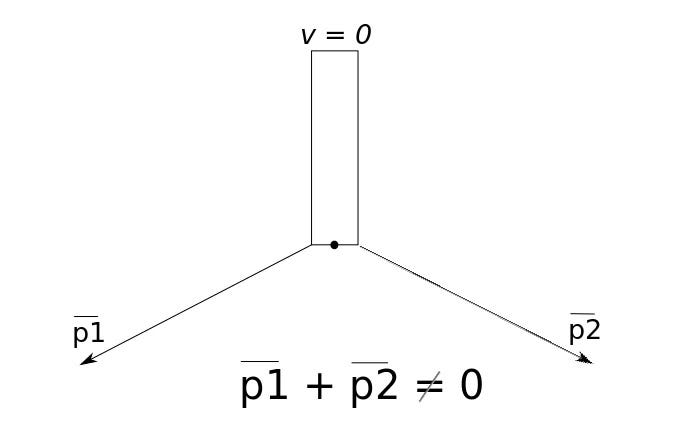
In the spacecraft's frame, the momenta of the emitted photons no longer cancel—resulting in a nonzero vector sum. Given that momentum conservation applies, the momentum of the emitted photons must derive from a change in the spacecraft's momentum. As established, momentum is defined as:

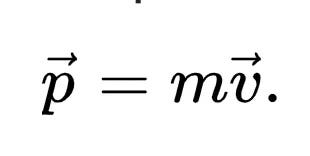
When photons are emitted, the spacecraft's velocity remains constant across all frames of reference, leading to a reduction in its inertial mass. By applying basic mathematical principles, we can deduce that the change in the spacecraft's mass correlates with the total energy of the emitted photons divided by the speed of light squared.

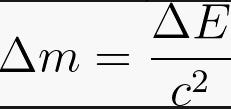
Now, envision a scenario where the spacecraft continues to emit photons until its entire inertial mass transforms into the energy of the emitted light. This thought process brings us to the celebrated equation:

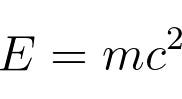
Through this reasoning, Einstein concluded that an object's inertial mass is equivalent to its energy.

Sources: A. Einstein. Does the energy of a body depend on the energy it contains? Bern, Switzerland, Ann. Phys., 18, 1905.

If you want to see more articles about space, feel free to subscribe to our channel and leave your questions, which I will address in future articles. Your support is invaluable, and you can help us enhance our content by becoming a member for just $5 a month.

Chapter 2: Exploring Video Perspectives on E=mc²

In order to grasp the nuances of E=mc², it can be beneficial to watch informative videos that elaborate on its implications.

The first video, titled "Why does E=MC²?" provides a comprehensive overview of the equation's significance in physics.

The second video, "Why E=mc² is wrong," presents a critical examination of the equation, offering alternative perspectives on its validity.