How to Tackle This Challenging Algebra Problem (XI) - Difficulty Level: Medium
Written on
Chapter 1 Overview of the Algebra Challenge
Welcome to the eleventh installment in our series on challenging algebra problems. As we conclude this year (2022) and look forward to the next (2023), I've encountered a particularly fitting algebra conundrum.
Multiple sources suggest that this problem originates from the Vietnamese International Maths Olympiad. However, I couldn't verify this claim or pinpoint its original source. With that settled, let’s dive into the mathematics; this should be enjoyable!
To start, we have the following set of equations:
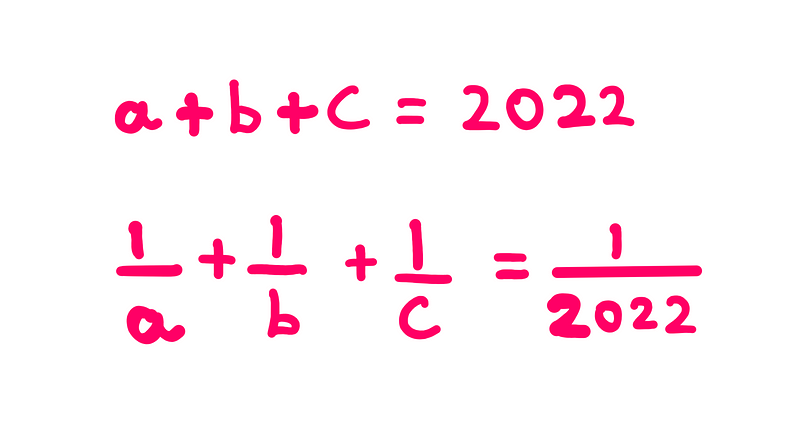
Your objective is to determine the solution for the following expression:
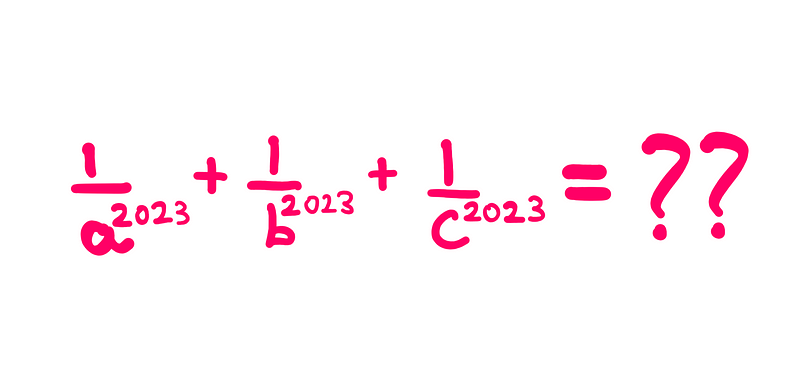
Do you believe you can crack this problem?
Spoiler Alert:
If you want to attempt solving this independently, I recommend pausing your reading here. After you’ve made your attempt, feel free to return and compare our methods. Good luck!
Setting Up the Problem
Let's label our initial set of equations as follows:
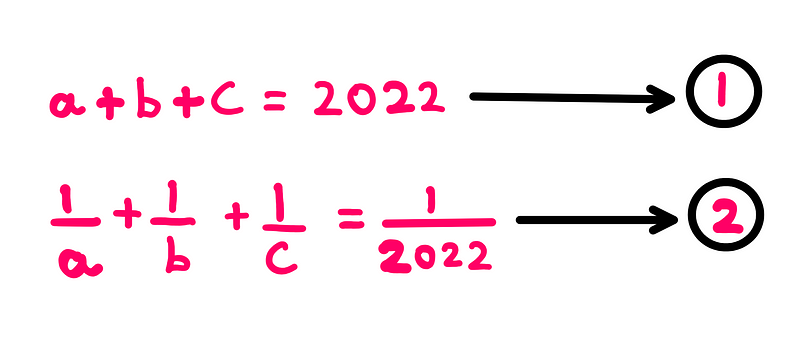
It's crucial to note that none of the variables a, b, or c can equal zero. If any of them were zero, equation-2 would become invalid due to division by zero. This subtlety is critical for our solution.
Now, let’s find a way to link equation-1 with equation-2. One straightforward approach is to reciprocate equation-1, as shown below (this is valid since (a + b + c) ≠ 0):
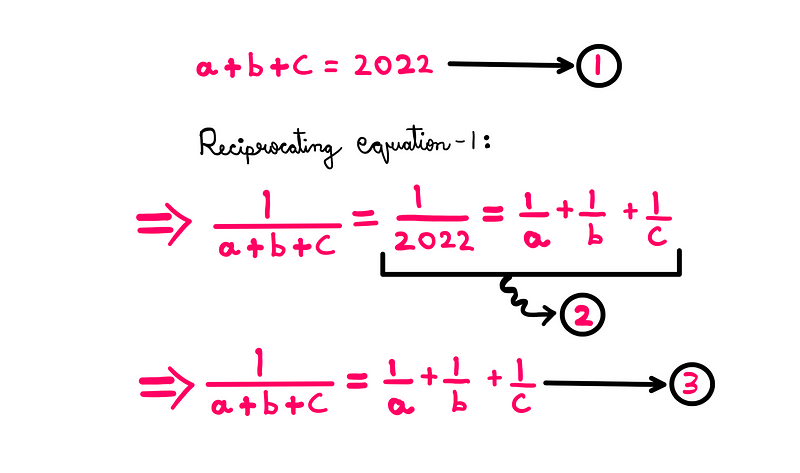
Next, we will manipulate equation-3 to consolidate all terms on the left side:
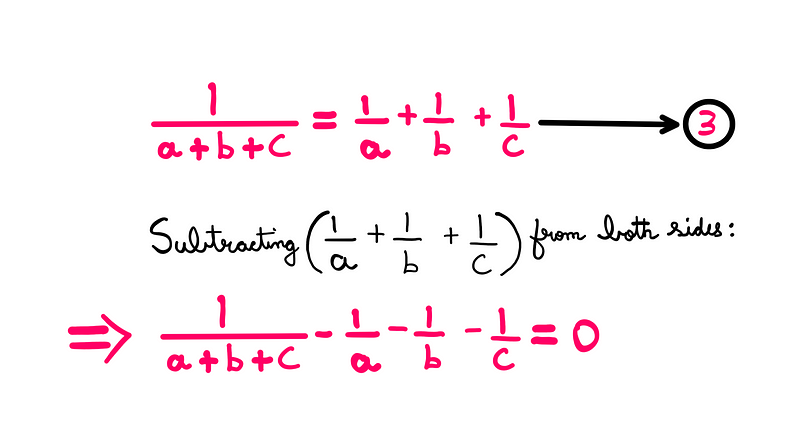
We can simplify the fractions further:
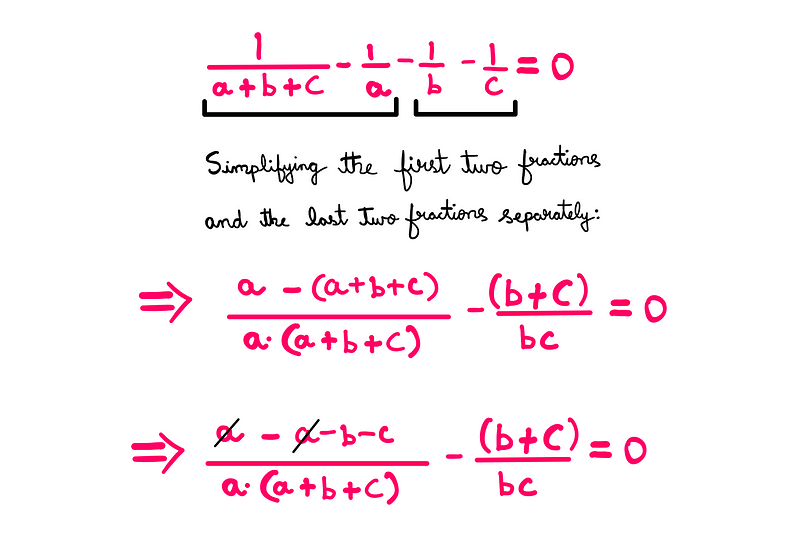
Continuing to simplify will allow us to eliminate the denominator (noting that (a*b*c) ≠ 0 from equation-2):
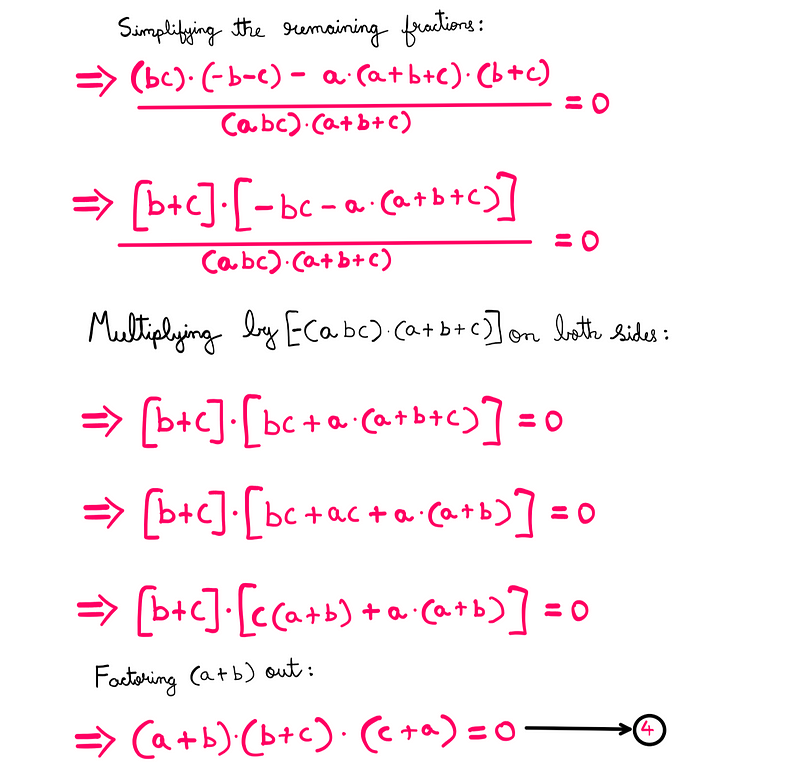
With equation-4 established, we are close to deriving our solution, but a few considerations remain.
Advancing the Solution
Equation-4 combined with equation-1 suggests that one of the following relationships must hold true:
(a = ±b) or (b = ±c) or (c = ±a).
Let’s assume (a = ±b). By substituting this into equation-1, we can determine the value for ‘c’:
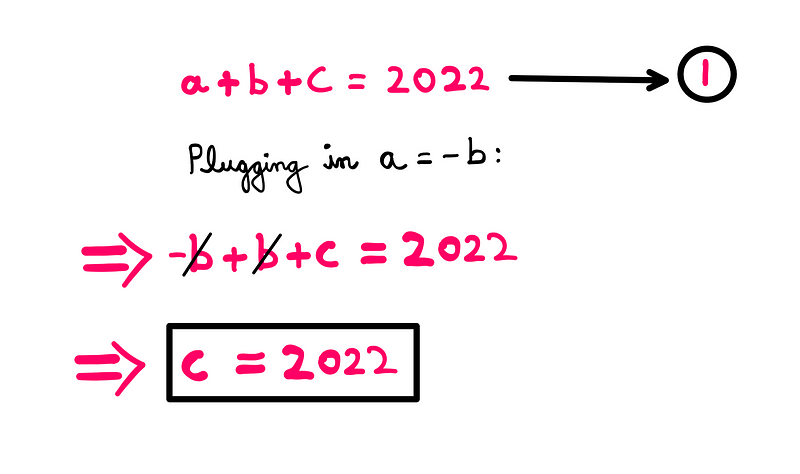
Next, we still need to find values for ‘a’ and ‘b’. For this, we can refer back to equation-2:
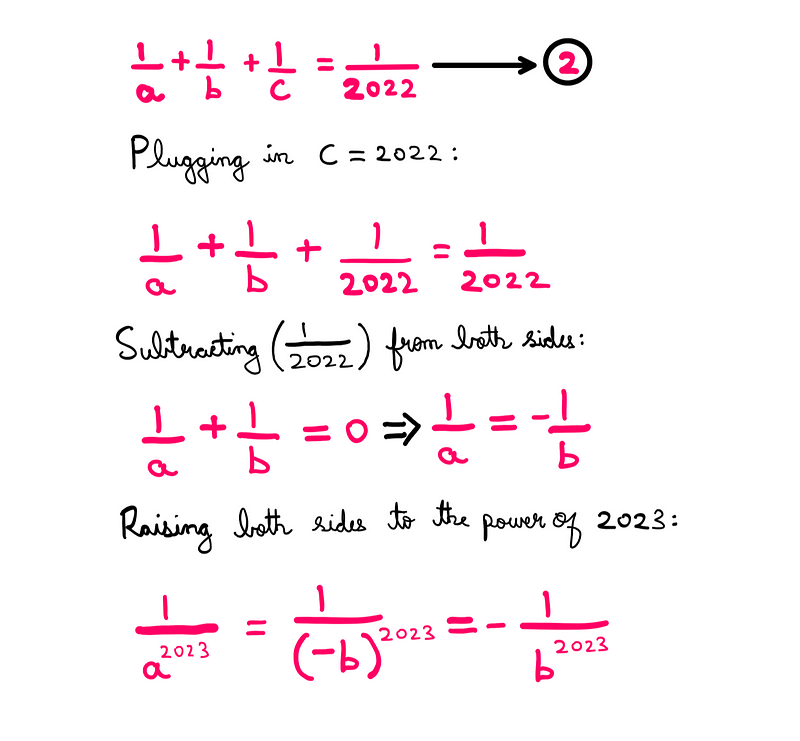
This leads us to our final solution for the problem.
The Final Answer to the Algebra Challenge
After our algebraic deductions, the solution is summarized as follows:
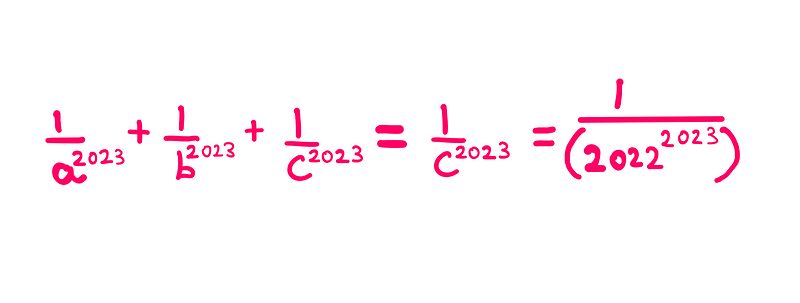
Remember, we initially assumed (a = ±b). We still need to evaluate the other two conditions: (b = ±c) or (c = ±a). Given the symmetric nature of the equation, regardless of which condition we analyze, two terms will cancel each other out, leaving one term remaining.
Thus, the generalized solution to our tricky algebra problem is expressed as:
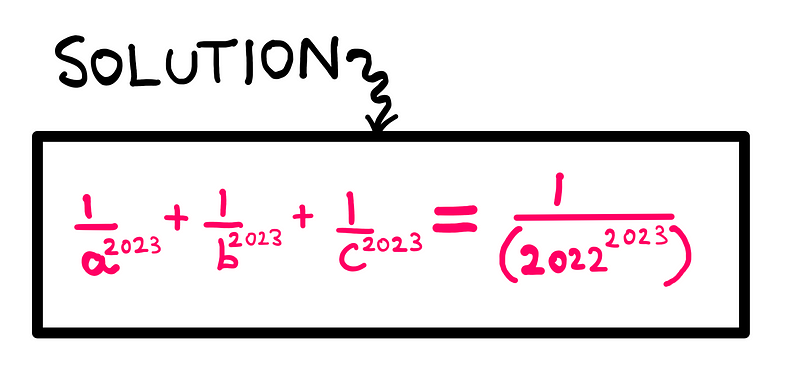
I hope you found this problem as intriguing as I did. Unfortunately, this marks the end of my algebra series for this year. However, stay tuned for more algebra challenges next year!
Explore Further:
If you're curious about similar problems, check out these insightful videos:
In the video, "Solving An INSANELY Hard Viral Math Problem," you will find a thorough breakdown of a complex algebra problem that has gained significant attention online.
The second video, "Equation Solving | 97% FAILED to answer this question | Algebra," presents a challenging equation that many struggle to solve, along with strategies for tackling it effectively.
If you’d like to support future content, consider contributing on Patreon. You can also read the original essay here.