Chapter 1: Introduction to the Mean Value Theorem

In this section, we will explore one of the foundational theorems in elementary analysis, known as the Mean Value Theorem. A basic understanding of derivatives is all that's necessary to grasp this concept.

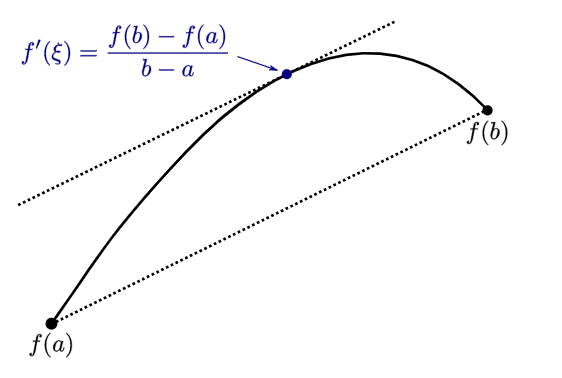
The theorem can be informally stated as follows: The straight line connecting the points (f(a)) and (f(b)) has a slope that equals the slope of the tangent line at some point (c) between (a) and (b). However, in mathematics, it is crucial to provide precise definitions along with visual representations, as images can sometimes lead to misconceptions. For instance, one might assume that the curve does not dip below the straight line joining (f(a)) and (f(b)).

Now, let’s present the formal definition. If a function is continuous and differentiable over the interval ([a, b]), then there exists a point (c) within that interval such that the following equation holds:

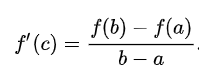
Chapter 2: The Proof of the Mean Value Theorem

The key to understanding this theorem lies in re-examining the function in question. Let’s consider the following function:

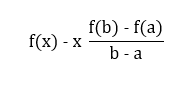
This new function, which we will denote as (g(x)), illustrates how much the function (f(x)) has increased compared to the line segment connecting points ((a, f(a))) and ((b, f(b))). Notably, the term ((f(b)-f(a))/(b-a)) represents the slope of the line connecting these two points.

At the endpoints (x = a) and (x = b), we can use basic algebra (feel free to verify this!) to show that (g(a) = g(b)). Since (g(x)) is continuous on ([a, b]), it must reach both a minimum and a maximum value within this interval, a characteristic of compact subsets in real analysis.

Now, we examine two scenarios:

Case 1: Maximum and Minimum at the Endpoints

If both the maximum and minimum values occur at the endpoints (x = a) and (x = b), then the function must remain constant across the interval ([a, b]). In simpler terms, if you consider a roller coaster that starts and ends at the same height, and that height represents both the maximum and minimum, then the height must remain unchanged throughout the ride. Consequently, (g(x)) is constant, leading to the conclusion that (f(x)) corresponds to the straight line connecting ((a, f(a))) and ((b, f(b))).

Case 2: Maximum or Minimum Occurs in the Interior

If either the maximum or minimum occurs at some point (c) in the interval, we know from calculus that the derivative at that point must equal zero. Let’s denote this point as (c).

We will first calculate the derivative:

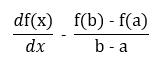
Next, we equate the derivative to zero at point (c) (Note the notation change from (frac{df(x)}{dx}) to (f'(x)) to indicate differentiation):

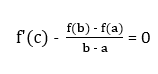
Ultimately, we arrive at the conclusion that at this point (c), we have:

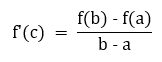
With this, we successfully complete the proof of the Mean Value Theorem.

Chapter 3: Visual Explanations

To enhance your understanding, please refer to the following videos.

The first video, titled "Proof of the Mean Value Theorem," offers a detailed explanation of the theorem's proof and its implications in calculus.

The second video, "Use Mean Value Theorem To Prove Inequalities," demonstrates practical applications of the theorem in establishing inequalities.