Chapter 1: Introduction to the Basel Problem

The Basel problem is a well-known challenge in mathematics, primarily concerning the sum of the reciprocals of the squares of integers. This intriguing question was first proposed by Pietro Mengoli in 1650 and later solved by the renowned mathematician Leonhard Euler in 1734, who demonstrated that the sum equals π²/6.

Chapter 2: Euler's Proof

To begin, we will examine Euler's method for solving the Basel problem. We start with the Maclaurin series expansion for sin(x) and, assuming x ≠ 0, divide both sides by x.

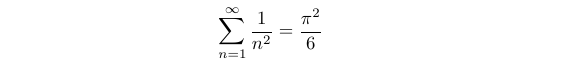
Euler then made the assumption that this infinite polynomial can be expressed as a product of its roots. While this assumption holds true in this context, it is not universally applicable to all polynomials.

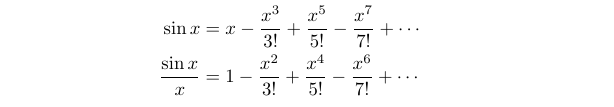
By comparing the Maclaurin series of sin(x)/x with the factored form, and substituting z = x², we arrive at the result for the Basel problem. This relies on the relationship between a polynomial’s coefficients and its roots, where the coefficient of the z term corresponds to the sum of the reciprocals of the roots.

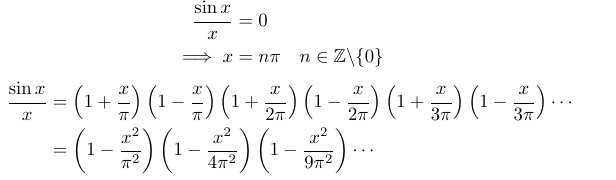
Although I won't elaborate on the final step of demonstrating that the sum of the reciprocals of the roots equals the z coefficient, it's worth noting that this can be effectively shown through induction with minimal effort.

Chapter 3: A Different Approach from STEP 3 2018

In this section, I will guide you through a problem from the STEP 3 2018 examination, which offers an alternative proof for the same result by considering limits of an inequality that bounds the sum of the reciprocals of the squares.

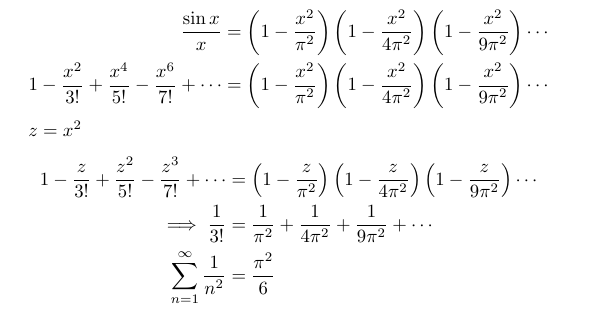
The Question

Before we dive into the solution, I encourage you to attempt the problem yourself.

Part (i)

In this initial section, we need to demonstrate a specific result. This becomes straightforward once we recognize that we can factor out 1/sin(θ) from the numerator of the left-hand side.

Next, we must identify the roots of the given polynomial, which requires some thought. The left-hand side of the result we established can also be expanded using the binomial theorem, revealing that the real terms cancel each other out.

Finally, by letting x = cot²(θ), we derive the original polynomial. This implies that the roots of the polynomial occur when

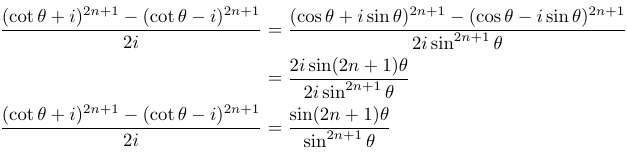
Note that since we set x = cot²(θ), we require x > 0, thus excluding the negative roots.

Part (ii)

This next part is relatively quick, as we simply apply the sum of roots formula for a polynomial.

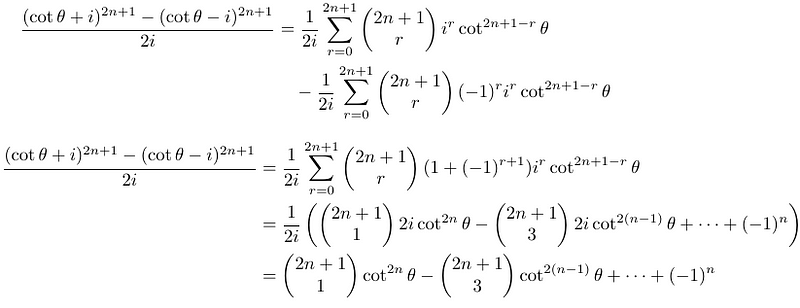
Not much effort is needed here, thankfully!

Part (iii)

For this section, we will square each term in the inequality and subsequently find the reciprocals of each component, ensuring we switch the inequality signs.

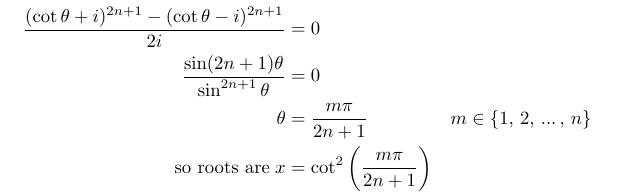
Now for the exciting part! We will utilize the proven inequality by letting θ = mθ/(2n + 1) and summing each part from m = 1 to m = n. Then, using the result from part (ii), we can substitute our findings into the cot²(θ) sums and rearrange. Finally, we take the limit as n approaches infinity.

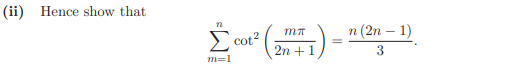
And there you have it! A remarkable result, along with an equally captivating proof.

Conclusion

Thank you for reading! If you have any thoughts or insights regarding this proof or the Basel problem, please feel free to share in the comments.

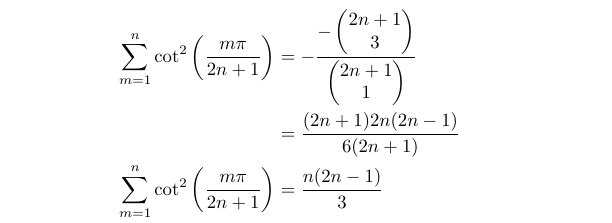
This first video, titled "Cauchy's Proof of the Basel Problem | Pi Squared Over Six," provides an engaging overview of Euler's proof. It highlights the significance of this mathematical milestone and explains the elegant reasoning behind it.

The second video, "If I did this in 1734 I'd be World Famous," offers a fascinating narrative on Euler's historical context and his groundbreaking contributions to mathematics. It sheds light on why the Basel problem remains a celebrated topic in mathematical circles.