Understanding Thales's Theorem: A Comprehensive Guide
Written on
Chapter 1: Introduction to Thales's Theorem
To grasp the essence of Thales's Theorem, let's visualize a circle:

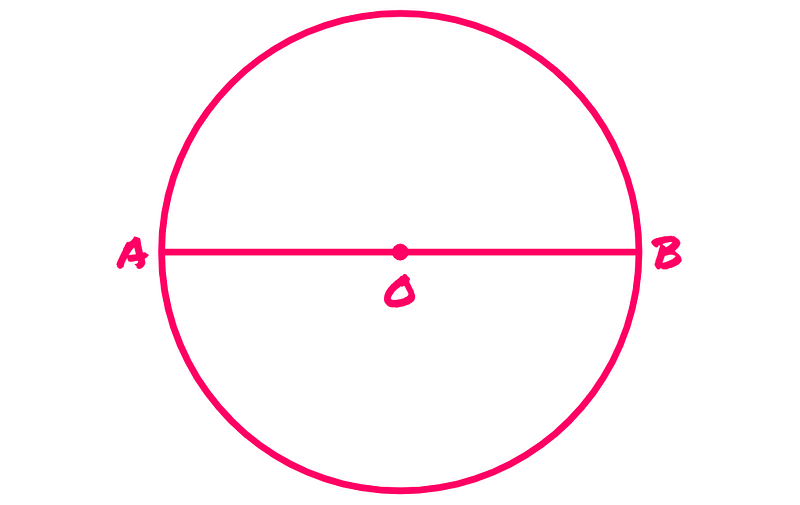
This circle has a center designated as O. Next, let’s draw a line through the center, ensuring its length matches the circle's diameter:
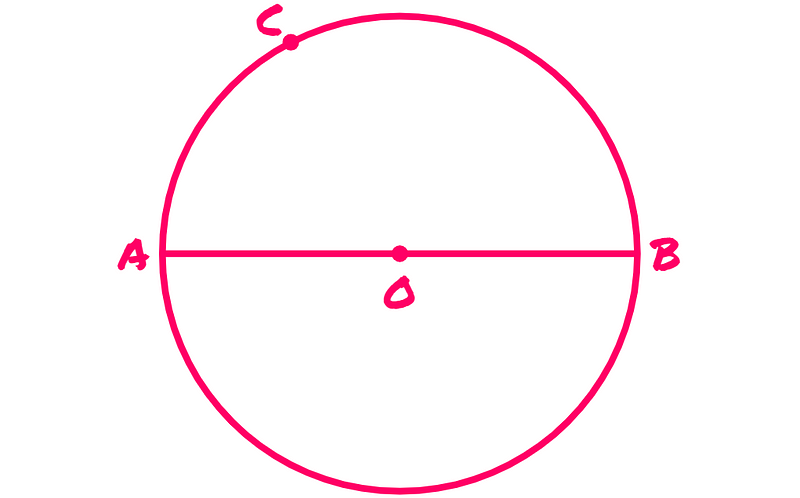
Now, select a point on the circumference of the circle (but not on the diameter) and label it C.
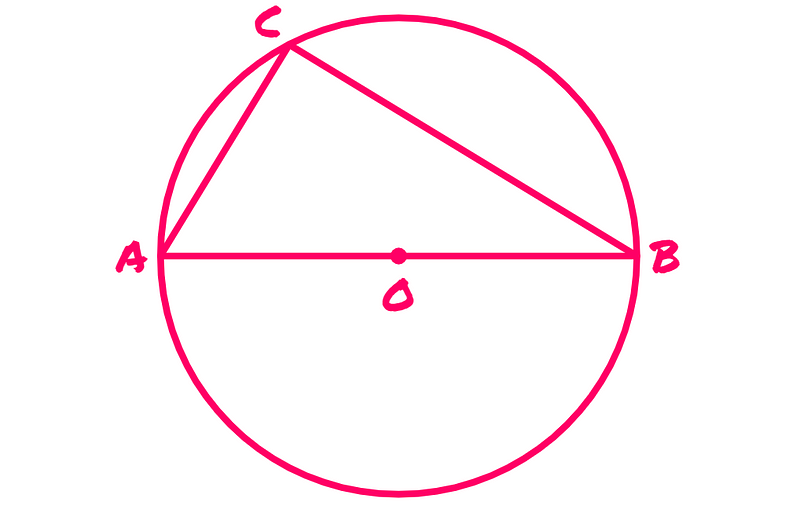
Next, we draw lines from A to C and from B to C, forming triangle ABC:
The question arises: what is the measure of angle ACB?
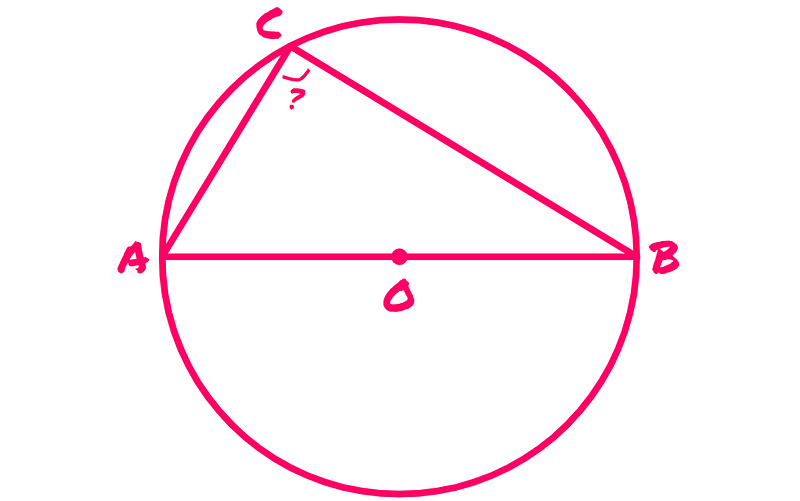
Let's examine our known elements. Since O is the midpoint of line AB, it follows that AO equals BO:
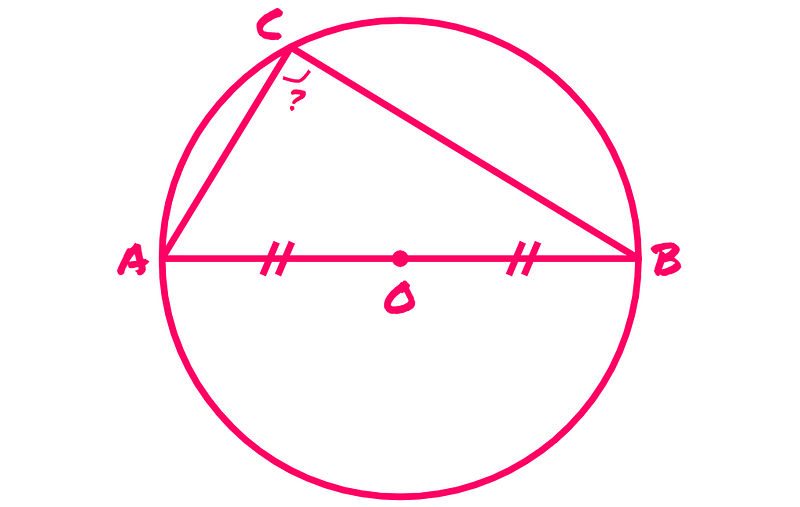
Furthermore, as point C lies on the circle, CO must also equal AO and BO:
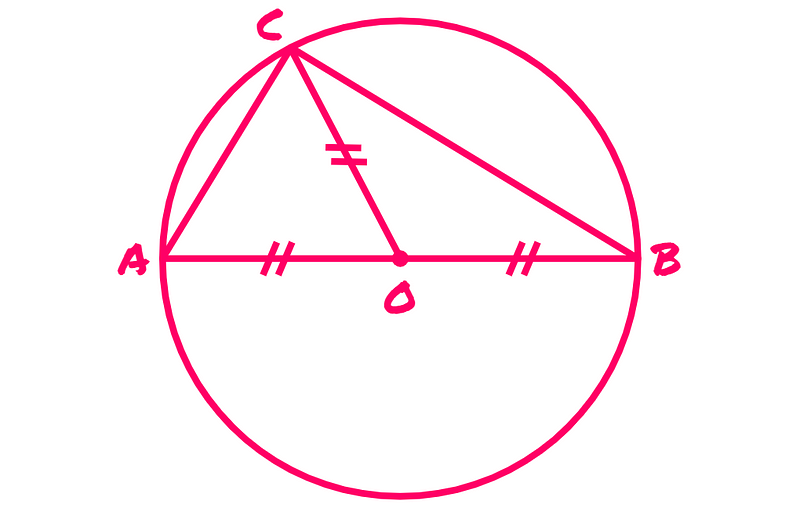
This establishes two additional isosceles triangles, ACO and BCO, where each has two sides of equal length. Consequently, the angles ∠ACO and ∠CAO are congruent, as are ∠BCO and ∠CBO:
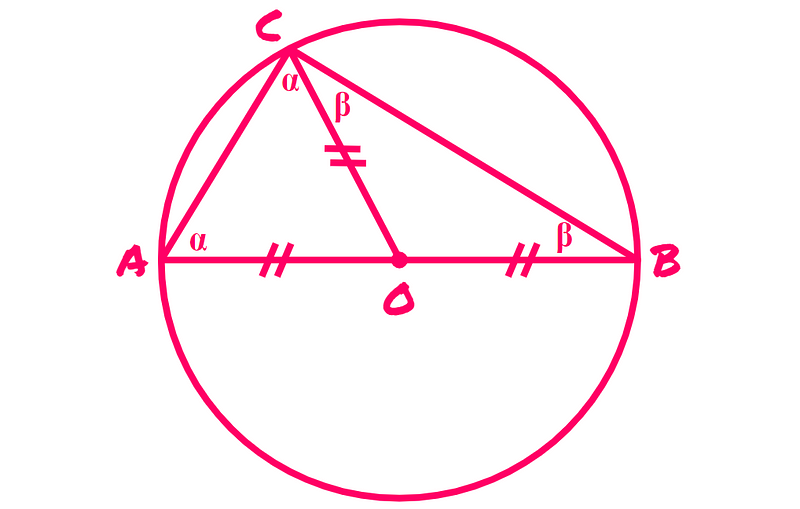
The sum of all interior angles in triangle ABC must equal 180°. Thus, we can express this as: ∠ + ∠ + ∠ + ∠ = 180°. Simplifying this gives us 2(∠ + ∠) = 180°, leading to ∠ + ∠ = 90°.
Note that ∠ + ∠ represents the angle ACB, which is precisely what we are trying to determine! Therefore, we conclude that the measure of this angle is 90°.
Our demonstration shows that this angle is consistently 90°, regardless of the position of point C on the circle (provided it's not located at A or B). In fact, whenever three distinct points A, B, and C are placed on a circle, and A and B create a straight line through the circle's center, it follows that ∠ABC will be 90°. This is the essence of Thales's theorem!
If you'd like to support Street Science, consider contributing through Patreon.
Chapter 2: Visualizing the Proof
For a deeper dive into the proof of Thales's Theorem, check out the following resources.
The first video, titled "What is the Proof for Thale's Theorem? | Minute Math," provides a concise explanation of the theorem and its implications.
The second video, "Thales' theorem proof," walks through the geometric proof step-by-step, enhancing your understanding of this fundamental concept in geometry.