Chapter 1: Math Game Highlights

A huge round of applause for the brilliant participants of our third weekly Math Game! 🎉

1st Place: William Keens - 7 Points 🏆

2nd Place: Carl Reiner Holdt - 5 Points 🥈

Other Participants: Neil Faver, Raveesh Sharma - 1 Point Each 🎖️

Here’s the solution to the challenge! 📝

Consider the polynomial ( P(x) = a ). Given that ( P(1) = P(3) = P(5) = P(7) = a ), we deduce that:

Applying the remainder factor theorem, we conclude that 1, 3, 5, and 7 are all roots of the polynomial ( P(x) - a ). If we let ( Q(x) ) represent the quotient of ( P(x) - a ):

This indicates that ( Q(x) ) is a polynomial with integer coefficients. The second condition states that ( P(2) = P(4) = P(6) = P(8) = -a ). Substituting these into the equation gives:

From this, we find:

[

-2a = -a - a

]

The integer coefficients of ( Q(x) ) are -15, 9, and 105. This implies that ( a ) must be divisible by 15, 9, and 105. We can determine the least common multiple:

[

text{lcm}(15, 9, 105) = 315 implies a text{ is a multiple of } 315.

]

Let’s define ( a = 315A ) for some integer ( A ). For example, if ( A = 2 ), then ( a = 630 ).

Now, let’s focus on ( Q(2) ) and ( Q(6) ):

Since ( Q(x) ) is derived from ( P(x) - a ), we can apply the remainder factor theorem to show that 2 and 6 are factors of ( Q(x) ):

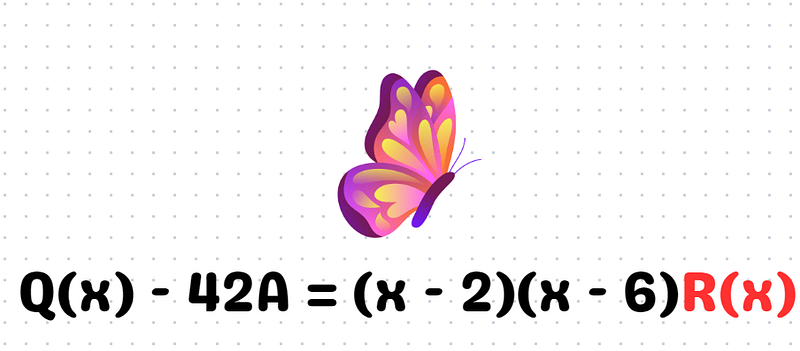
Next, we will evaluate ( Q(4) ) and ( Q(8) ) separately. Utilizing similar reasoning as before, we find:

This simplifies to:

[

R(4) = 28A, quad R(8) = -4A

]

We aim to formulate a generalized polynomial ( R(x) ) that includes factors ( (x - 4) ) and ( (x - 8) ). One suitable expression is:

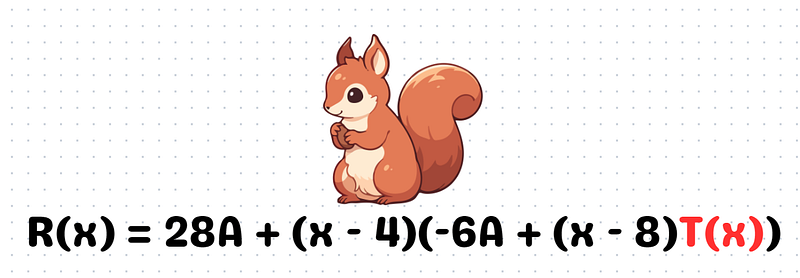
Here, ( T(x) ) is a polynomial with coefficients. Thus far, we have created an expression for ( P(x) ) that can be expressed in terms of ( (x - 1), (x - 3), (x - 5), (x - 7), (x - 2), (x - 4), (x - 6), ) and ( (x - 8) ).

It’s essential to note the relationships: ( T(x) ) is within ( R(x) ); ( R(x) ) is contained in ( Q(x) ); and ( Q(x) ) is part of ( P(x) ). We will substitute ( R(x) ) back into ( Q(x) ) and subsequently into ( P(x) ).

By substituting back, we find that:

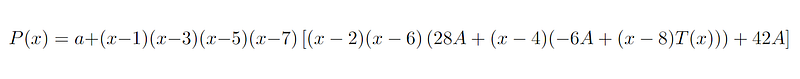
Notice that substituting 1, 3, 5, and 7 into ( P(x) ) yields ( P(x) = a ), while substituting 2, 4, 6, and 8 provides ( P(x) = -a ). This polynomial holds for all integers ( A ) and any polynomial ( T(x) ).

Recalling that ( a = 315A ), it’s minimized when ( A = 1 ):

The solution is B!

How did you fare in the third weekly Math Games? Looking forward to seeing you next week, challengers! 🎊

Chapter 2: Understanding Polynomial Coefficients

In this video, we explore the leading coefficients and degrees of polynomials, crucial concepts for understanding polynomial behavior in mathematical contexts.

This video covers the roots and coefficients of polynomial equations, providing insights into their interrelationships and significance in problem-solving.