Exploring Integrals with Respect to dx²: A Calculus Challenge
Written on
Chapter 1: Understanding the Integral
In calculus, we typically handle integrals in the form of f(x)dx, where dx signifies a minuscule change in x. But how do we approach an integral like d(x²)? Today, we will unravel this interesting question.
Generally, if we denote y = f(x), then we have dy = f’(x)dx.
Take a moment to reflect on this statement! Grab your pen and paper to give it a shot before continuing. Once you're ready, let's move on to the solution!
Solution
When y is a function, dy represents its differential. We can utilize the aforementioned rule to determine the differential of d(x²).
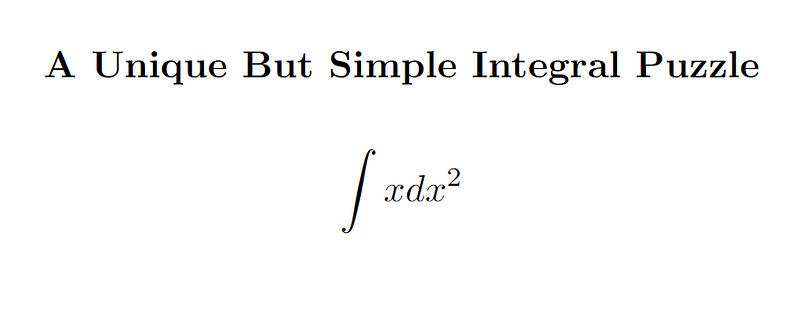
Having differentiated x² with respect to dx, can you see the direction we're heading in? Indeed, the initial rule we discussed arises from interpreting the differential operator as a fraction!
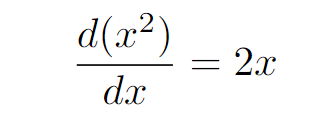
At this point, we’ve transformed what seemed like a complex integral into a more manageable one.
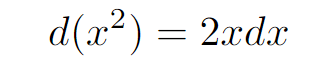
Next, we can further streamline the process and apply the reverse power rule.
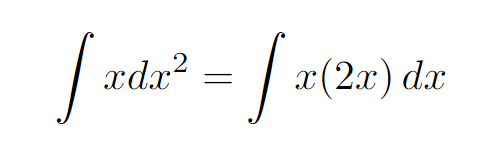
And remember to include the constant c! That concludes our solution.
Isn’t it fascinating?
What were your thoughts while solving this? I’d love to hear from you in the comments below!
Math Puzzles
Explore an array of engaging math puzzles available on Medium, covering topics such as Algebra, Geometry, Calculus, and Number Theory. Share these with your friends and dive into the fun of problem-solving!
The first video, "ECZ: How to find d²y/dx² and the integration of a function," offers a comprehensive explanation of finding derivatives and integrals, which can enhance your understanding of these concepts.
In the second video, "Math for fun#16, 2nd derivative rule?", the presenter breaks down the second derivative rule in an engaging way, making complex ideas more accessible.
Thank you for taking the time to read this article! If you found it helpful, please consider clapping for it.
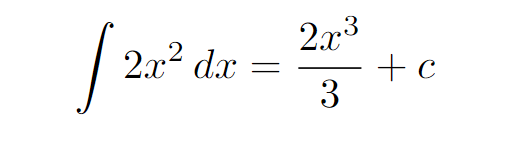
If you enjoy my content, consider buying me a coffee to support my writing journey. Your generosity is greatly appreciated!
Happy Solving, Bella