Chapter 1: The Dangers of Misguided Data Fitting

Recently, I encountered a troubling question on ResearchGate. The inquiry presented a dataset and sought methods for fitting it to a model. A multitude of suggestions emerged, ranging from polynomial and logarithmic fits to square root functions. However, no one paused to consider what the data actually represented.

This lack of inquiry is alarming. It’s entirely possible to find a model that will conform to a given dataset, and in fact, there are countless models capable of doing so. Remarkably, an infinite number of polynomials can fit a finite set of points!

Therefore, we must be discerning in our model selection. To achieve this, we need to reflect on how our variables should behave. For instance, if we have three variables affecting poverty rates, does it make logical sense for the rate to be negative or exceed 100%? Similarly, if we’re analyzing two variables, x and y, why should we restrict ourselves solely to linear models of the form y = mx + b? What justifies our assumption of linearity?

As scientists, it’s crucial to remember that our goal is to model reality, not merely to fit data. We must always consider the underlying processes that produce the data. In the example I mentioned earlier, the individual was attempting to model absorption over time. While the specifics were unclear, knowing we are modeling absorption is significant. Why?

The reasoning is straightforward. An absorbent material has a finite capacity for absorption. Thus, as it absorbs more, its ability to take in additional substance diminishes. In essence, the absorption rate begins at its peak and gradually decreases to zero as saturation occurs. The anticipated rate and solution are depicted below:

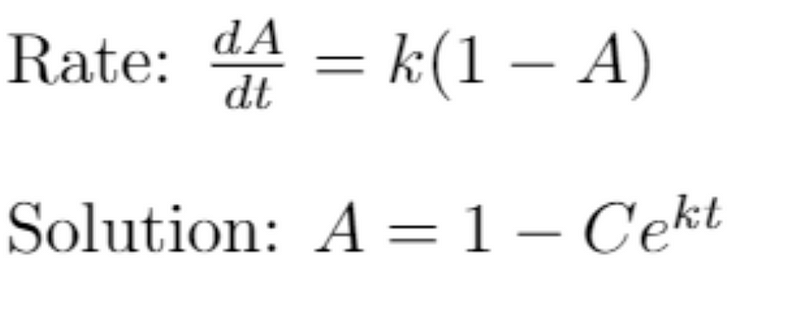
Consequently, we would expect an exponential function that approaches one asymptotically. The data supports this expectation, providing us with a solid rationale for confidence in our model. While the fit might not be flawless, our objective shouldn't simply be to find a function that yields a good regression fit.

It’s important to clarify that examining a dataset to discern its general shape can be valuable, especially when the relationships between variables are ambiguous. However, if we attempt to match graphs to the entire dataset without a guiding principle, we lack justification for our choices later on. We can always discover a model that appears to fit “really well,” but it’s essential to seek models that have intrinsic meaning. Failing to do so leads to poor scientific practices.

Chapter 2: Upholding Standards in Scientific Communication